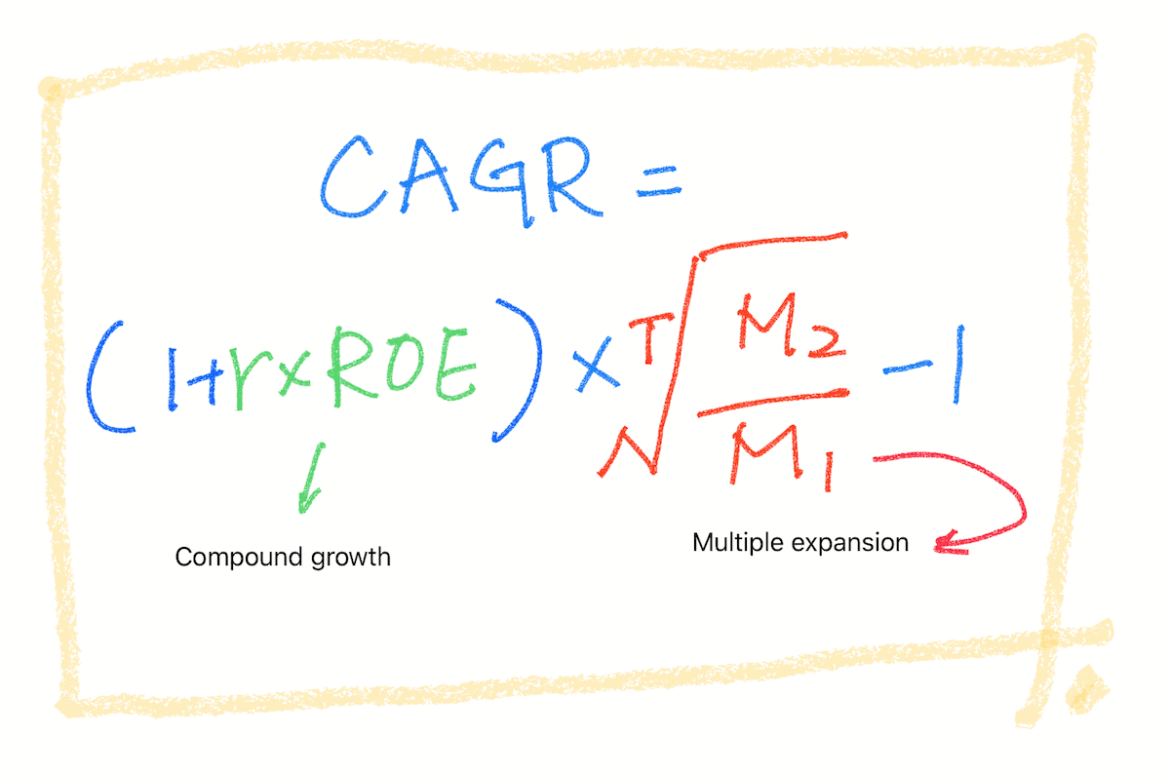
本篇文章的中文標題應該是:「估計長期投資年複合報酬率的數學方程式」,因為這十幾個字實在太累贅了,葛八不得已只好簡化成「報酬方程式」,讓標題言簡意賅點。如果你看到這個方程式的第一點是有點嚇到、想關機,那千萬不要,因為看懂這個方程式對理解「長期投資」、「compound growth 複合成長」、市場的「multiple expansion 估價倍數」乃至整體報酬率的影響很重要,這個數學方程式幫助葛八了解長期投資的概念助益匪淺,葛八非常想要分享給你。
這個公式的導法及來源來自這篇不知名作者的文章,原先作者的公式是如圖左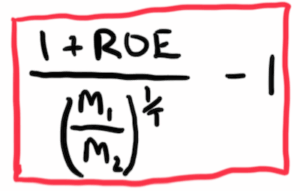 ,考量一般人對除法較難以親近的認知,葛八改成了下圖以乘式為主的公式,這樣較易於了解。其中的 T 代表投資持有總年數;M 是 multiple,M1 是指投資當年的本益比,M2 是賣出時的本益比;r 是 reinvestment percentage 再投資比率1;g 是複合成長率,也就等於 r×ROE。為了便於解說,葛八在圖中的公式中,用藍色字體代表公式主體,用綠色字體部分來說明 compound growth 複合成長 r×ROE;用紅色字體來說明市場 multiple expansion 對投資報酬率的影響。
,考量一般人對除法較難以親近的認知,葛八改成了下圖以乘式為主的公式,這樣較易於了解。其中的 T 代表投資持有總年數;M 是 multiple,M1 是指投資當年的本益比,M2 是賣出時的本益比;r 是 reinvestment percentage 再投資比率1;g 是複合成長率,也就等於 r×ROE。為了便於解說,葛八在圖中的公式中,用藍色字體代表公式主體,用綠色字體部分來說明 compound growth 複合成長 r×ROE;用紅色字體來說明市場 multiple expansion 對投資報酬率的影響。
這樣的公式怎麼使用呢?(以下案例僅為教學示範,並不是投資建議,請見葛八的免責聲明):
示範案例一:
台灣 5871 中租-KY這家公司,過去五年的平均 r (reinvestment percentage 再投資比率)大約是 58%,平均 ROE 大約是 16.5,目前的本益比 (2025/09) 大概是 9。因為投資是投資未來,假設你現在投資 5871 這家公司,預計持有 15 年,就你對中租的了解,你認為未來 15 年的平均 r 和 ROE 、本益比會跟現在差不多,也就是當 15 年後你會實現獲利。那麼套入公式,大概這 15 年你的投資年複合報酬率是:(1+0.6×16.5)× (10/10)^(1/15)-1= 10%(數字均經過四捨五入),以這樣的年複合報酬率大約你投入的資金 15 年後會穩穩的成長到 4.2 倍(未計入股息和配股)。
示範案例二:
CPRT 是一家在美國 NASDAQ 上市的公司,它的主營業務是「經手報廢車的回收、買賣」。CPRT 過去十年的平均 r (reinvestment percentage 再投資比率)大約是 87%(從來不發放股息、偶爾進行股票回購),過去 10 年平均 ROE 大約 22%,目前 (2025/09) 的本益比大約是 28 倍。假設你現在開始投資 CPRT,預計持有 15 年。你預計未來 15 年 CPRT 的平均 r 和 ROE 跟現在差不多,但是第 15 年你準備 cash out 賣出時,本益比會微調上升到 30 倍(畢竟能夠長期維持 ROE 20% 的公司並不多)。套入公式,大概這 15 年你的投資年複合報酬率是:(1+0.87×0.22)×(30/22)^(1/15)-1= 1.2 ×1.02-1= 21.5%,以這樣的年複合報酬率大約你投入的資金 15 年後會穩穩的成長到 19 倍(未計入股票回購)(這顯示出長期投資在具有持久競爭優勢公司的威力)。
當然每個投資人對公司的了解不同,對未來的預期數據自然不同,經過計算的結果也會不同。
好,了解公式的粗略用法後,葛八要來一項項拆解長期投資收益最大化的祕密武器,以及你要怎麼思考它。
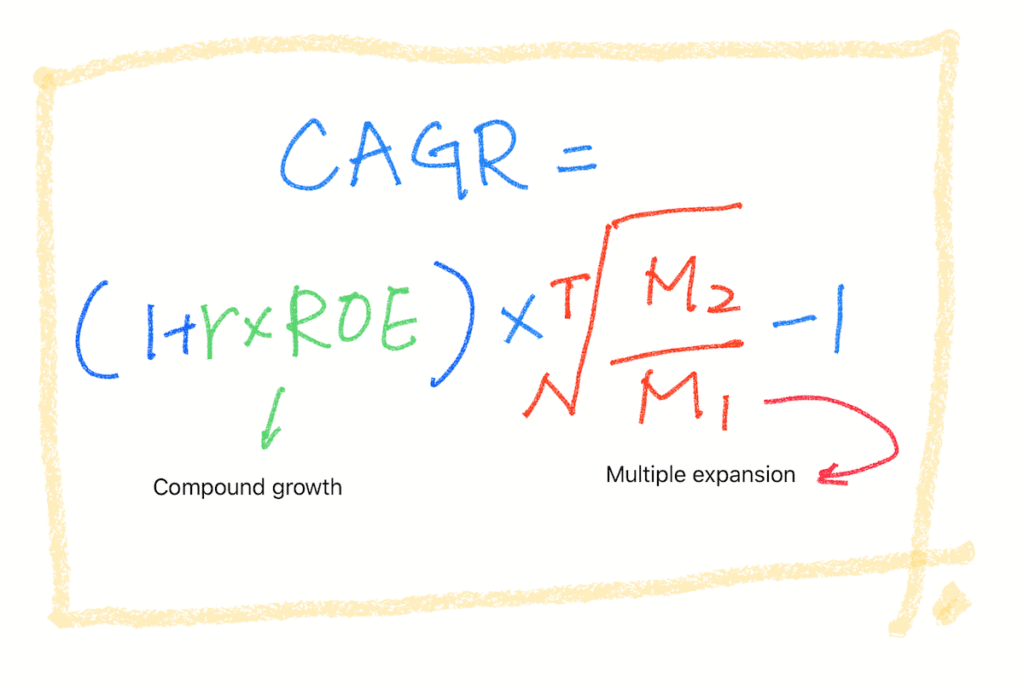
T= year, M= multiple, M1= purchase multiple, M2= multiple when selling, g= growth, r= reinvestment percentage
CAGR Compound Annual Growth Rate 年複合成長率
以投資來說,年複合成長率也可以稱為「年化投資報酬率」,如果你已知道對任何一項投資的終值(也就是賣出後總值),假設中間沒有再投入新的資金,那麼你的年化投資報酬率就很容易計算(感謝 Andy Lin)。那「 Andy Lin 的 IRR 公式」跟葛八這篇文章介紹的「The Mathematics of Returns 長期投資年複合報酬率的數學方程式」又有什麼關係?感覺越來越混亂了?!
如果搞不清楚,就回來看大家都知道的銀行存款的案例,台灣的活期存款是用來思考「複利」很方便的的類比,那篇文章的案例中,我們假設了一個年利率 15% 的活期存款,且每年配出一半的利息,剩下的一半利息歸回本金中繼續利滾利。葛八喜歡「利滾利」(或是「錢滾錢」)這類的名詞,因為這代表了「複利」。
葛八列出的「估計長期投資的年複合報酬率的數學方程式」,藍色字體部分是這個方程式的主結構,這個主結構怎麼導出來,葛八已經建議各位去看原作者的說明了,而這個方程式在等號的右邊包含了兩個部分,分別是綠色字體代表了公司(或是任何投資)幫你複利的速度,以及紅色字體部分代表了市場價格對投資報酬率的影響,這兩部分是用一個相乘符號連結,代表兩項因素都影響你的成績單。
接下來,讓葛八分開說明。
綠色字體 r\times ROE
有一種投資,不會受到市場價格的干擾,很適合說明 r×ROE,那就是葛八所舉的「特殊的銀行存款」的例子。大部分的銀行活期存款,是可以讓你「所有的利息」都可以用來「利滾利」的,葛八所舉的案例是以規定只有「部分利息可以再投資」的特例,就是模擬大多數的公開市場的公司,很少是 100% 保留盈餘的,或多或少都會以股票回購或是現金股利的模式回饋股東,只是保留的比例不同罷了。
這也是葛八在「什麼代表公司的成長率?」文章中主要想要表達的重點:r×ROE 代表公司成長率,也代表了公司幫你複利的速度,而配息出來的部分,也屬於你的收益,但是這部份就沒有參與複利的機制了。
銀行存款的案例就是幫你了解這部份,我們再回來看一下這個特殊銀行存款的案例:
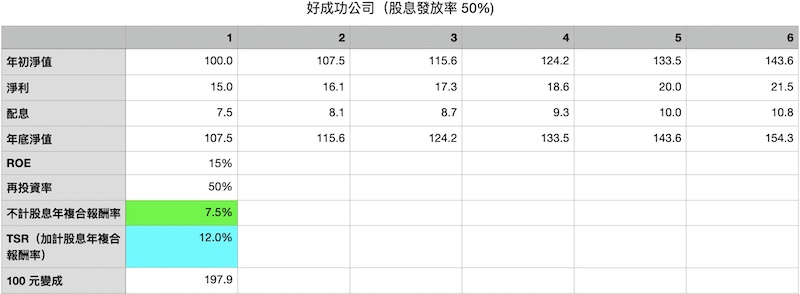
在這個案例中,你有兩部分的收益,一部分是配息出來的部分,這部份隨著配息相對於原始投資的比例越來越高(第一年股息殖利率是7.5%,第二年提高為 8.1%,到了第六年的股息到達 10.8%),你可以了解到配息出來的部分,雖然配出的股息沒有辦法以 15% 的利率來複利長大,但也還可以接受。第二部分的收益就是沒有配出的淨利,這部份是以 15 % 年複合報酬率的速度長大。
綜合上述兩者,你到了第六年的年複合報酬率大約是 12%(藍色儲存格數字)。也許你會覺得 12% 也不錯啊?!但是你要知道如果你的公司完全不配息,百分百保留來複利(極端的案例),你的年複合報酬率是 15%。
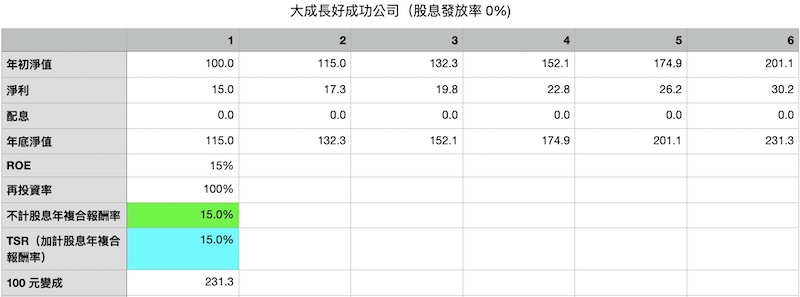
換句話說,假設市場價格比不變動,當 r= 100%,長期投資一家公司的投資複合報酬率大致上就等於公司的 ROE。
而 12% 和 15% 複利的差別是:
投資 1 萬元,以 12% 複利 15 年,結果是 54,736 元。
投資 1 萬元,以 15% 複利 15 年,結果會是 81,370 元。
這也是葛八不喜歡發股息的原因,希望公司發揮全力幫我複利。很多人雖然了解發出的股利是「昂貴的奢侈品 (an expensive luxury)」2、發出的股利沒有複利的功能(股息是單利),但是因為擔心「公司賺的錢不是錢、發出來拿在手上的錢才是錢」,所以寧願放棄複利,選擇單利。
但是葛八卻相信:經過精心挑選的好公司,賺的每一分錢都是實實在在的錢,寧願讓它複利,也不要選擇單利。
紅色字體 \sqrt[T]{M2/M1}
第二部分我們要討論的部份是「市場估價倍數對投資報酬率的影響」,也就是公式中紅色字體的部份。
長期投資減輕估價倍數萎縮的影響
大多數人的都有:聽到別人說是好公司後、認出這是好公司的能力,也就是葛八在投資人接收的 3 種資訊等級這篇文章中所說的 Level 0 投資。當然有些投資人可以發現一些 Level 1 投資,也就是股價還沒有起飛之前,業績已經開始顯示潛力的公司,但是在這個人云亦云的時代,Level 1 投資是極少見的,更遑論有機會成為百倍股的 Level 2 投資。
要知道,大家都耳熟能詳、朗朗上口的好公司,唯一的缺點是價格很難被低估。這種公司的本益比,長期持有的話,大概率向下的機會會遠大於往上提高的機會。
所以葛八假設一個極端的狀況:期初投資的本益比是 40 倍,期末獲利了解時本益比下降到 10 倍,我們來套入文中公式紅色字體的部份:
投資期 3 年:(10/40)^(1/3)= 0.63, 代表我們前一段所說的複利機制要再被打 63 折。
投資期 15 年:(10/40)^(1/15)= 0.91,代表我們前一段所說的複利機制只被打了 91 折。
代表投資期拉長到 15 年,即便投資初期買到相對高價(相對於盈餘,本益比萎縮 4 倍)的錯誤決策,你所受到的「估價倍數降低」對年化報酬率的影響會大大的被鈍化。事實上,如果你願意把投資期拉更長,這樣的公式對你的錯誤更寬容。
| PE 本益比縮小 4 倍 | 3 年 | 10 年 | 15 年 | 30 年 | 100 年 |
|---|---|---|---|---|---|
| M1: M2= 40: 10 | 0.63 | 0.87 | 0.91 | 0.96 | 0.99 |
當然葛八看不出來投資 100 年這種「為子孫而投資」的意義是什麼,即便它幾乎可以弭平市場價格對你年化報酬率的影響。你們可以套用不同的「市場估價倍數」、「投資年期」來得到不同的數據。
當然,你也可以試試「投資倍數放大 4 倍」這樣的假設。
投資期 3 年:(40/10)^(1/3)= 1.59, 代表我們前一段所說的複利機制可以放大 1.6 倍。
投資期 15 年:(40/10)^(1/15)= 1.1, 代表我們前一段所說的複利機制只被放大 1.1 倍。
| PE 本益比放大 4 倍 | 3 年 | 10 年 | 15 年 | 30 年 | 100 年 |
|---|---|---|---|---|---|
| M1: M2= 10: 40 | 1.6 倍 | 1.15 倍 | 1.1 倍 | 1.05 倍 | 1.01 倍 |
你可以看到,長期投資也沖淡了「市場本益比放大」對年複合報酬率效果的助力(時間是公平的)。
從公式來思考「最大化年複合投資報酬率」的策略
葛八曾經在達成百倍投資的兩種策略方案提到兩種達到 10- 100 倍股的方案:
每 3 年達成 26% 的報酬率,連續 7 次
第一種是每三年換一次股,設法將這 3 年內的投資報酬率最大化,連續 7 次。這 3 年內,如果你可以使用最大的 r 再投資百分比、最大的 ROE(最大化你的 compound growth 複利成長,公式圖中綠色部分),而你的估價倍數(比如說本益比放大 4 倍)會對「compound growth 複利成長」有放大 1.6 倍的效果(multiple expansion 估價倍數放大,圖中紅色部分)。
這樣的作法,相當困難。本益比放大本來就不容易,還要連續找到七次本益比在 3 年內都放大的公司更難。這種作法的優點是因為估價放大的效應較大,公司的 r× ROE 可以相對的輕鬆點。
買進一家 26% 報酬率的公司,持有 20 年
第二種方法是只投資一家公司,從公司默默無名開始投資,過程中參與公司的複利成長(最大的「 r 再投資百分比」,這時 ROE 也逐漸開始提高,最大化你的 compound growth 複利成長,公式圖中綠色部分),這過程中,你的 multiple expansion 估價倍數也在 20 年內逐步放大(公式圖中紅色部分,例如文中舉例本益比擴張 4 倍,雖然說拉長投資期到 20 年,沖淡了這個放大的效果,但至少是放大,不是縮小)。
這個方法對公司的品質要求較高,需要較高的 r×ROE,且需要你找到尚未被廣泛關注(本益比尚低)的公司。
Christopher Mayer 的 twin engines 雙引擎效應
在 Christopher Mayer 的尋找百倍股書中提到一個名詞: twin engines 雙引擎3效應,這個名詞很容易的可以由葛八本篇文章所分享給你的公式來理解。
想要收穫多、百倍股,你必須有最大的 「compound growth 複利成長」,也要取得最大的「multiple expansion 估價倍數」。想要達成這兩項,你要找到相對小的公司(複利成長機會大),擁有未來的、潛在的競爭優勢且別人看不懂的公司(同時享受本益比放大的優勢)。
想想看,這樣的公司不會是現在的 TSLA 特斯拉, 10 年前的 TSLA 會是;不會是現在的 AMZN 亞馬遜,20 年前的 AMZN 會是,不會是現在的 BRK.A 波克夏·海瑟威,30 年前的 BRK.A 會是。
如果你只會投資現在大家耳熟能詳的公司,你可能會賺錢,甚至可能賺幾倍的投資收益,但幾乎沒有機會收穫百倍股!
長期投資人的思考
PE multiple 對長期投資人的影響
我們再來看一個表格,這個數據是假設我們長期投資 20 年,PE multiple 對投資報酬率的影響。要了解 PE multiple 是市場對標的公司喜愛程度的表徵,葛八分別假設獲利了結時的 PE multiple M2 分別是投資時 PE multiple M1 的 1/4 (代表標的被市場冷落)、1/2、不變、2 倍、4 倍(賣出時市場對標的是狂熱的)的情況下,對 r*ROE 的放大/縮減的效果。
| t=20 年 | 市場變冷落 | 不變 | 市場變高調 | ||
|---|---|---|---|---|---|
| PE multiple 放大/縮小 (M2/M1) | 1/4 | 1/2 | 1 | 2 | 4 |
| 對 r*ROE 的影響 | 0.93 倍 | 0.97 倍 | 1 | 1.04 倍 | 1.07 倍 |
| 假設 r*ROE=15, CAGR= | 7% | 11.5% | 15% | 19.6% | 23% |
從表中可以看出,PE multiple 的放大、縮小對我們的公司複利能力 (r*ROE) 扮演放大縮小的效果,表格中 PE multiple expansion 到 4 倍算是相對極端的案例(買的時候本益比 10 倍,賣的時候變成 40 倍),它的確對投資報酬率有明顯的影響。
長期投資人賺的是 r*ROE,本益比放大是錦上添花
市場情緒是長期投資人無法掌握的,而選對好公司是我們的責任,負責最大化 r*ROE 是我們投資人有可能做到的。本益比放大的是錦上添花、雪中送炭還是割你一塊肉走,這有很大的部份要靠運氣了,我們只知道投資時不要買貴了,但畢竟長長 20 年,你怎麼知道市場先生會怎麼想?!
好了,最後葛八想要請你再看一次公式:
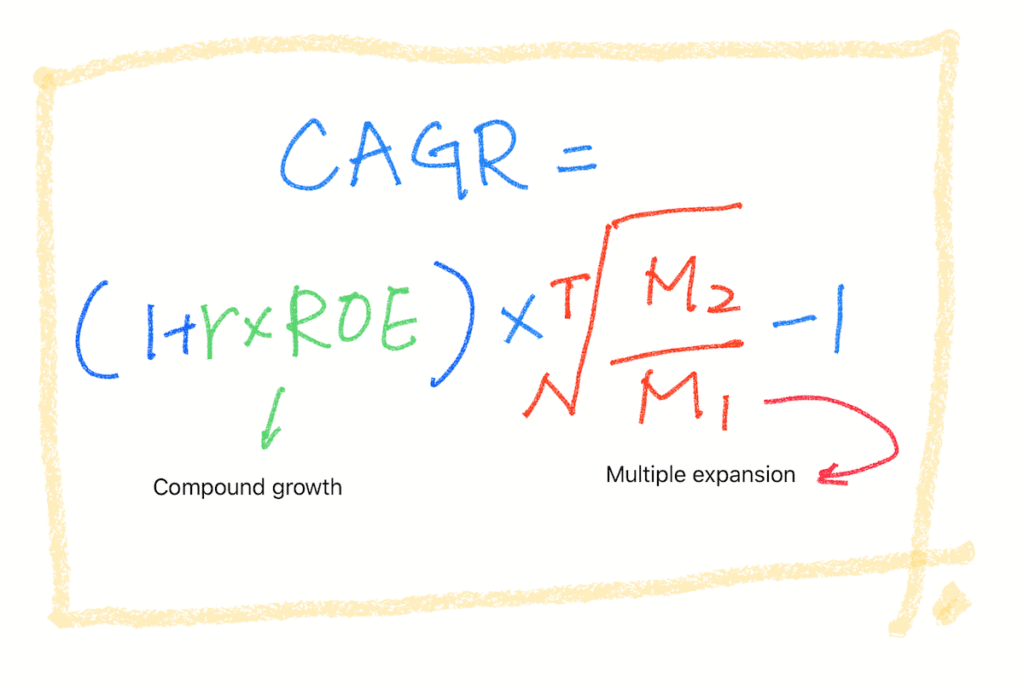
T= year, M= multiple, M1= purchase multiple, M2= sold multiple, g= growth, r= reinvestment percentage
投資人要拉高年複合投資報酬率需要的是:最大的「 r 再投資比例」、最高的「ROE 報酬率」(綠色部分)、最長的「 T 複利時間」及需要擁有相對於「買進本益比」的最大「賣出本益比」(紅色部分),就像公式中告訴你的那樣!
(本篇完)
Footnote 註釋:
- Reinvestment percentage 有些作者會用 reinvestment rate 來說明,但因為常常跟 reinvestment rate (of return) 相混淆,所以葛八使用 reinvestment percentage,而中文翻譯是再投資比率。計算再投資比率,只要計算一段期間內的保留盈餘差額除以該期間的淨利和,就代表這段期間公司總共賺了多少錢,其中有多少保留在公司的比率。以複利成長來說,r 值越大,好公司幫我們複利的能力越強。 [↩]
- 原文是:Dividends are expensive luxury.,出自 Thomas Phelp 的書「100 to 1 in the stock market」。[↩]
- Twin 雙引擎代表的是兩部分的共同效果,第一部分是盈餘成長 earning growth(公式圖中綠色部分),第二引擎是估價倍數放大(公式圖中紅色部分)。Christopher Mayer 在該書的中文版的第 56, 68, 71, 264 頁都提到這個效應:最大化你的投資收益,才有機會收穫百倍股。[↩]